对数不等式的解法
a>1时,logf(x)>logg(x) f(x)>g(x)>0
f(x)>g(x)>0
0af(x)>logg(x) 例1 若不等式|ax+2|<6的解集为(—1,2),则实数a等于( ). A.8 B.2 C.—4 D.—8 分析 本题考查了简单的绝对值不等式的解法以及含参不等式的分类讨论思想. 解 由|ax+2|<6知—6 若解集为(—1,2),则a>0时, 须有 a<0时须有 评析 本题也可采用代入检验法. 例2 解不等式:(1)2x—x—15x>0; (2)(x+4)(x+5)(2—x)<0. 分析 可用标根法求解,但要处理好重根的情况. 解 (1)原不等式可化为x(2x+5)(x3)>0, 把方程x(2x+5)(x—3)=0的三个根x=0,x=—5/2,x=3顺次标上数轴, 然后,从右上方向左下方开始画曲线顺次经过三个根,其解集如图的阴影部分. ∴原不等式解集为{x|—5/2 (2)原不等式等价于(x+4)(x+5)(x—2)>0 ∴原不等式解集为{x|x<—5或—5 评析 用“标根法”解不等式时应注意:①各一次项中x的系数必为正②对于偶次或奇次重根可参照(2)的解法转化为不含重根的不等式,也可直接用“标根法”,但注意“奇穿偶不穿”,其法如图. 例3 解下列不等式 (2) 分析 (1)将不等式同解变形为3<3的形状,再将其等价转化为f(x) (2)利用换底公式将不等式转化为t=logx的不等式求解. 解 (1)原不等式 ∴原不等式的解集为(—1,4) (2)令t=logx,则原不等式可化为 ∴原不等式的解集为 解不等式 例4 分析 由于对数函数的增减性与底数a的取值范围有关,因此应分为01两种情形讨论该不等式的解集,其次,在去对数符号时要注意同解性,不等式变形时,还要注意同解性. 解 为了使不等式有解,必须a>0且a≠1. (1)当a>1时,原不等式等价于不等式 (2)当0 综上所述,当a>1时,不等式的解集为 0
0 且
且 无解.
无解.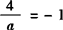 ,且
,且 知a=—4,故选C.
知a=—4,故选C.

 ,
,

 .
.
 —1
—1 1)
1)

 ,
,
 .
.

 ;当0.
;当0.
-

- 严嵩与反转天下的风水师
- 一、深谋远虑嘉靖年间,内阁首辅严嵩痴迷风水命理,深信堪舆方术之说。有一次皇上因为京城下水道不畅,大雨时总引发涝灾,准备进行整修,严
-

- 荀子如何教导楚庄王治理国家?
- 荀子是如何教导楚王治理国家的呢?其中有这么个故事。楚庄王听说荀子是当世的大儒,便派人向他请教怎样才能把国家治理好。儒学荀子听
-

- 对董卓的评价
- 三国志作者陈寿评曰:“董卓狼戾贼忍,暴虐不仁,自书契已来,殆未之有也。”后汉书评曰:“董卓初以虓阚为情,因遭崩剥之埶,故得蹈藉彝伦,毁裂
-

- 华元劝晋国、楚国休战
- 晋国、楚国两大国之间连年征战,各自损失极为惨重。宋卿华元得知晋、楚两国有谋求媾和之意,就主动出来斡旋,促成晋、楚结盟。华元不但
-

- 晋文侯威胁最大的不是其弟“成师”,而是殇叔
- 周宣王的时候,晋国国君是晋穆公,穆公的太子叫仇,后来又生了个小儿子成师。《左传》和《史记》都记录说,当时就有个叫师服的贤大夫发表
-

- 九天玄女的传人
- 九天玄女是九天的圣主,中华民族是九天玄女的传人,《诗经? 商颂 ? 玄鸟》有 “天命玄鸟,降而生商”, 我还认为,通过 “玄鸟 ” ,得知 “天