反函数
式子y=f(x)表示y是自变量x的函数,设它的定义域为A,值域为C,我们从式子y=f(x)中解出x,得到式子x=φ(y).如果y在C中的任何一个值,通过式子x=φ(y),x在A中有惟一的值和它对应,那么式子x=φ(y)就表示x是自变量y的函数.这样的函数x=φ(y),叫做函数y=f(x)的反函数,记作x=f(y).
1.反函数存在的条件
若函数y=f(x)的定义域为A,值域为C,且函数所确定的映射是A到C的一一映射,则该函数存在反函数.
2.原函数与反函数的关系
(1)函数y=f(x)的定义域、值域分别是反函数y=f(x)的值域、定义域.而反函数的定义域必须通过求原函数的值域得到.
(2)一般地,函数y=f(x)的图象和它的反函数y=f(x)的图象关于直线y=x对称.
(3)图象间的关系:y=f(x)与x=f(y)是同一图象,而y=f(x)与y=f(x)图象关于直线y=x对称.
3.求一个函数f(x)(x∈D)的反函数分三个步骤:
(1)由y=f(x)解出x=f(y);
(2)x、y位置互换,得到y=f(x);
(3)标明反函数定义域(即原函数值域).
4.两个有用的结论
(1) .
.
(2)f[f(x)]=x,x∈f(x)的值域,
f[f(x)]=x,x∈f(x)的定义域.
5.函数与反函数的关系(如下表)

例1 求下列函数的反函数:

分析 按求反函数的方法分步求解.

易知在x≤—1时,函数是递减函数,存在反函数,对原式两端平方,得y=x+x,

∴ 且原函数的值域为{y|y≥0}.
且原函数的值域为{y|y≥0}.
故所求的反函数为

(2)当0≤x≤1时,—1≤x—1≤0,
即—1≤y≤0.
由y=x—1(0≤x≤1)得 ,
,
∴ .
.
当—1≤x<0时,0 由y=x(—1≤x<0)得 ∴ 综上所述 例2 若点(1,2)既在函数f(x)= 分析 利用互为反函数的两个函数图象之间的关系. 评析 由于互为反函数的函数图象关于直线y=x对称,因而点(1,2)在反函数f(x)的图象上时,其关于直线y=x的对称点(2,1)必在原函数的图象上. 例3 已知 解 ∵y=g(x)的图象与y=f(x+1)的图象关于直线y=x对称, ∴y=g(x)与y=f(x+1)互为反函数.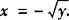 .
. .
.
 的图象上,又在其反函数f(x)的图象上,试确定f(x)的解析式.
的图象上,又在其反函数f(x)的图象上,试确定f(x)的解析式.
 ,函数y=g(x)的图象与f(x+1)的图象关于直线y=x对称,求g(11)的值.
,函数y=g(x)的图象与f(x+1)的图象关于直线y=x对称,求g(11)的值. 的反函数为f(x)=
的反函数为f(x)= .
.

-

- 川岛芳子或是双性恋 遭日本养父强奸改变性取向
- 资料图:川岛芳子戎装照在日本的谍海中,“巾帼女豪们”的手段丝毫不逊于男子,而这些女谍中的头号人物,无可争议的当数川岛芳子。她的活
-

- 秦穆公:羊皮换贤
- 秦穆公(?─前621),名任好,春秋时期秦国国君。自幼便胸怀大志,于公元前659年即位,他在位期间,内修国政,外图霸业,任人唯贤,使国势逐渐强大起来
-

- 九天玄女的传人
- 九天玄女是九天的圣主,中华民族是九天玄女的传人,《诗经? 商颂 ? 玄鸟》有 “天命玄鸟,降而生商”, 我还认为,通过 “玄鸟 ” ,得知 “天
-

- 董仲舒斥孟子
- 董仲舒与孟子的学术之争是鲜为人知的,可能许多人不相信,但这却是真实的。董仲舒画像这天,几只蜜蜂正在董宅后院飞来飞去忙着采蜜。董
-

- 晋襄公漏言害两臣!领导泄密可咋整?
- 公元前621年,晋国准备和狄国开战,晋襄公拟派狐夜姑(一作射姑)为主将,赵盾做副将,带兵出征。晋襄公画像晋襄公:(公元前621年):姬姓,讳欢,谥号曰
-

- 召公遗物召公簋讲述的往事
- 2006年11月,陕西省扶风县城关镇五郡西村发现一座西周时期的青铜器窖藏,出土器物27件(组)。其中两件带有铭文的五年琱生尊最为重要,